평면 좌표 경로 압축 알고리즘
2D 평면 좌표(x, y)들의 경로를 압축, 요약하는 알고리즘을 만들어보자.
사전 지식
이 알고리즘은 평면좌표 표현 방법과 기초 삼각 함수를 숙지하여야 한다.
라디안
라디안 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 라디안(영어: radian)은 각의 크기를 재는 SI 단위이다. 호도(弧度)라고도 하며, 기호는 rad이다. 단위원의 중심각의 라디안 값은 그 각이 대하는 호의 길이와 같다. 1라디안은 약 57.3도이다. 라디안은 입체각의 단위인 스테라디안과 함께 SI 보조 단위에 속했으나, 1995년에 SI 보조 단위가 폐지되면서 SI 유도 단위가 되었다. 라디안의 표기는 rad 기호가 가장 흔하며, 이는 자주 생략된다. 간혹 c(위첨
ko.wikipedia.org
Math.atan2 개요
[프로그래밍 이론] 두 점 사이의 절대각도를 재는 atan2
두 점 사이의 절대각도를 재는 atan2 프로그래밍 언어에서 역탄젠트를 계산하는 함수 atan2의 특징을 알아보자 아크탄젠트란? 아크탄젠트(arctangent)는 역탄젠트라고도 하며 탄젠트의 역함수이다. ��
spiralmoon.tistory.com
이 알고리즘이 필요한 이유
좌표 경로 압축 알고리즘은 경로를 표시할 때 좌표 목록을 압축해야하는 경우에 쓰인다.
예를 들어 좌표 경로가 정확한 일직선인 경우, 모든 좌표를 표현하지 않고 시작좌표와 끝좌표만으로도 경로를 충분히 그릴 수 있기 때문에 그 사이의 의미없는 좌표를 없애므로써 경로를 좀 더 간결하게 표현할 수 있다.
또한, 좌표 경로를 화면으로 그려야 하는 경우(특히 모바일 앱) 좌표 목록이 너무 많아지면 draw 과정에 렉이 걸리기 때문에 이를 간추려야 할 때에도 쓰인다.
알고리즘의 전제 조건
좌표 경로 압축 알고리즘의 전제 조건은 세 가지다.
첫 번째, 비슷한 방향으로 경로가 진행되면 이 경로를 잇는 좌표들을 추려낼 수 있다.
두 번째, 비슷한 방향으로 경로가 진행되는지는 이전 좌표와 현재 좌표의 각도를 재면 알 수 있다. 각도가 일치구간 허용치를 초과하면 다른 방향, 초과하지 않으면 비슷한 방향으로 판단한다.
세 번째, 처음 좌표와 마지막 좌표는 반드시 기록한다.
두 점 사이의 각도 구하기
좌표의 진행 방향을 구하기 위해서는 두 좌표간의 각도를 구해야한다.
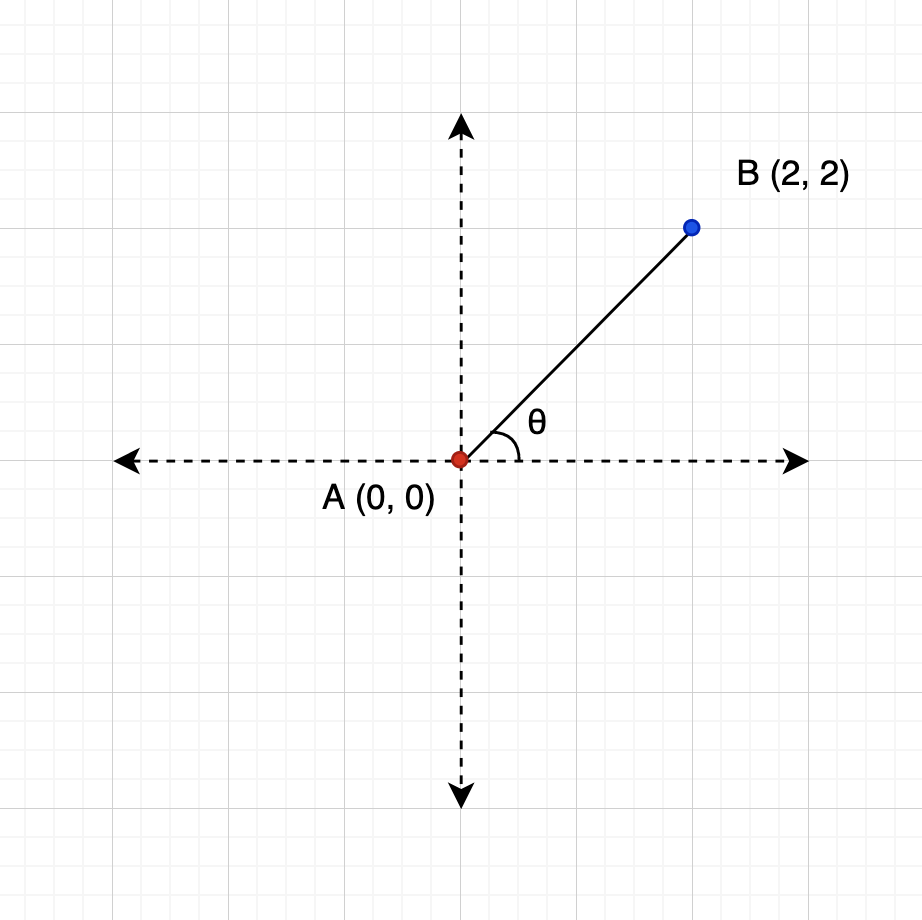
두 점 A(0, 0)와 B(2, 2)가 있다. 우리가 구해야 하는 값은 A에서 B로 경로가 진행될 때의 θ 값이다. θ 값은 A를 기준점으로 한 B의 상대좌표를 알면 구할 수 있다.
const A = {
x: 0,
y: 0
};
const B = {
x: 2,
y: 2
};
// A를 기준점으로 한 B의 상대 좌표(길이)
const relativeCoordinateX = B.x - A.x;
const relativeCoordinateY = B.y - A.y;
상대좌표를 얻었다. 이 때 tanθ는 relativeCoordinateY / relativeCoordinateX 이므로 θ를 구하기 위해선 역탄젠트(arctangent)를 취해주어야 한다.
프로그래밍 언어에선 역탄젠트 함수 atan과 atan2를 지원하고 있다. 이 글에선 atan2를 사용해서 각도를 구할 것이다.
// A를 기준점으로 B와의 라디안을 구함
const radian = Math.atan2(relativeCoordinateY, relativeCoordinateX);
// 라디안 값을 각도로 변환
const degree = radian * 180 / Math.PI;
atan2 함수를 사용해서 A를 기준점으로 B까지의 절대각을 구할 수 있다. 위 코드를 실행하면 θ는 45°가 된다.

일치구간 각도 허용치(threshold) 조절하기
좌표 A에서 B를 향하는 경로의 절대각을 구할 수 있게 됐으므로, 반복문을 이용하면 여러 좌표간의 절대각을 구할 수 있을 것이다.
우선 여러 좌표간의 절대각을 계산하여 출력하는 코드를 작성해보자.
// 여러 좌표의 목록. 경로는 인덱스 순서를 따른다.
const paths = [
{ x:0, y:0 },
{ x:2, y:2 },
{ x:5, y:3 },
{ x:3, y:5 },
{ x:-2, y:4 },
{ x:-1, y:3 }
];
for (let i = 0; i < paths.length - 1; i++) {
const relativeCoordinateX = paths[i + 1].x - paths[i].x;
const relativeCoordinateY = paths[i + 1].y - paths[i].y;
const radian = Math.atan2(relativeCoordinateY, relativeCoordinateX);
const degree = radian * 180 / Math.PI;
console.log(degree);
}
이 소스코드의 실행 결과는 다음과 같다.
45
18.43494882292201
135
-168.6900675259798
-45
이를 평면좌표계로 그렸을 때

위와 같은 그림이 나온다.
그렇다면 좌표 경로 압축 알고리즘의 핵심인 "비슷한 방향인지 판단"을 어떻게 할까?
정답은 B 좌표의 절대각이 A 좌표의 절대각으로부터 일치구간 허용치 범위 내에 있는지를 검사하면 된다. 초과한다면 다른 방향으로 판단하고, 초과하지 않으면 비슷한 방향이라고 판단하는 것이다.
일치구간 허용치를 10°라고 가정해보면 paths[0]의 절대각을 기준으로 했을 때, paths[1]의 절대각이 45° ± (10 / 2)° 범위 안에 들어야 paths[0]과 paths[1]가 비슷한 경로라고 판단할 수 있는 것이다.
정리하자면, 위 그림에서 paths[1]의 절대각은 18.43°이며,
일치구간 허용치가 10°일 때 => 이는 45° ± (10 / 2)°의 범위 안에 들지 못하기 때문에 비슷하지 않은 경로다.
일치구간 허용치가 60°일 때 => 이는 45° ± (60 / 2)°의 범위 안에 들기 때문에 비슷한 경로다.
허용치는 반드시 0° ~ 180° 이어야 한다. (180 = ±90, 180°는 원의 절반)
이 알고리즘에서는 허용 구간이 클수록 경로의 정확도는 떨어지지만 압축률을 올릴 수 있으므로 적당히 조절해주는 것이 필요하다.
알고리즘 적용
최종 알고리즘은 다음과 같다.
// 예시 좌표 목록. 경로는 인덱스 순서를 따른다.
const paths = [
{ x:0, y:0 },
{ x:1, y:1 },
{ x:3, y:2 },
{ x:5, y:3 },
{ x:8, y:2 },
{ x:9, y:2 },
{ x:9, y:3 },
{ x:8, y:4 },
{ x:4, y:5 },
{ x:3, y:7 },
{ x:3, y:8 },
{ x:4, y:11 },
{ x:5, y:12 },
{ x:7, y:13 },
{ x:9, y:13 },
{ x:10, y:13 },
{ x:12, y:13 },
{ x:13, y:12 },
{ x:14, y:10 },
{ x:15, y:8 },
{ x:13, y:7 },
{ x:14, y:6 },
{ x:16, y:5 },
{ x:18, y:5 },
{ x:19, y:5 },
{ x:24, y:4 },
{ x:26, y:3 },
{ x:25, y:2 },
{ x:22, y:0 },
{ x:21, y:-1 },
{ x:18, y:-2 },
{ x:14, y:-3 },
{ x:11, y:-4 },
{ x:10, y:-4 },
{ x:7, y:-5 },
{ x:5, y:-5 },
{ x:2, y:-4 },
{ x:0, y:-3 },
{ x:-2, y:-1 },
{ x:-3, y:1 }
];
// 일치구간 한계치.
const threshold = 20;
// 압축된 좌표 목록.
const newPaths = [];
// 첫 번째 좌표는 무조건 압축 목록에 포함시킨다.
newPaths.push({ x: paths[0].x, y: paths[0].y });
let prevDegree = null;
for (let i = 0; i < paths.length - 1; i++) {
const relativeCoordinateX = paths[i + 1].x - paths[i].x;
const relativeCoordinateY = paths[i + 1].y - paths[i].y;
// 라디안
const radian = Math.atan2(relativeCoordinateY, relativeCoordinateX);
// 절대각
const degree = radian * 180 / Math.PI;
// 현재가 첫 좌표라서 이전 좌표의 절대각이 없는 경우
if (prevDegree === null) {
prevDegree = degree;
continue;
}
// 현재 좌표가 이전 좌표로부터 일치구간을 벗어난 경우
if (overRange(degree, prevDegree, threshold)) {
newPaths.push({x: paths[i].x, y: paths[i].y});
prevDegree = degree;
}
}
// 마지막 좌표는 무조건 압축 목록에 포함시킨다.
newPaths.push({ x: paths[paths.length - 1].x, y: paths[paths.length - 1].y });
/**
* 현재 각이 이전 각으로부터 일치구간을 벗어나는지 검사
*/
function overRange(degree, prevDegree, threshold) {
const fullAngle = 360;
// 최대 허용값, 최소 허용값을 정의
let maxDegree = prevDegree + (threshold / 2);
let minDegree = prevDegree - (threshold / 2);
let newDegree = degree;
// 최대 & 최소 허용값이 atan2의 범위를 벗어나는 동시에
// 현재각과의 기호(+-)가 다르면 계산이 불가능하기 때문에 음수인 쪽에 360을 더하여 양수로 보정
if (maxDegree >= (fullAngle / 2) && newDegree < 0) {
newDegree += fullAngle;
} else if (minDegree <= -(fullAngle / 2) && newDegree > 0) {
maxDegree += fullAngle;
minDegree += fullAngle;
}
// 범위 초과 여부
return minDegree > newDegree || newDegree > maxDegree;
}압축 결과
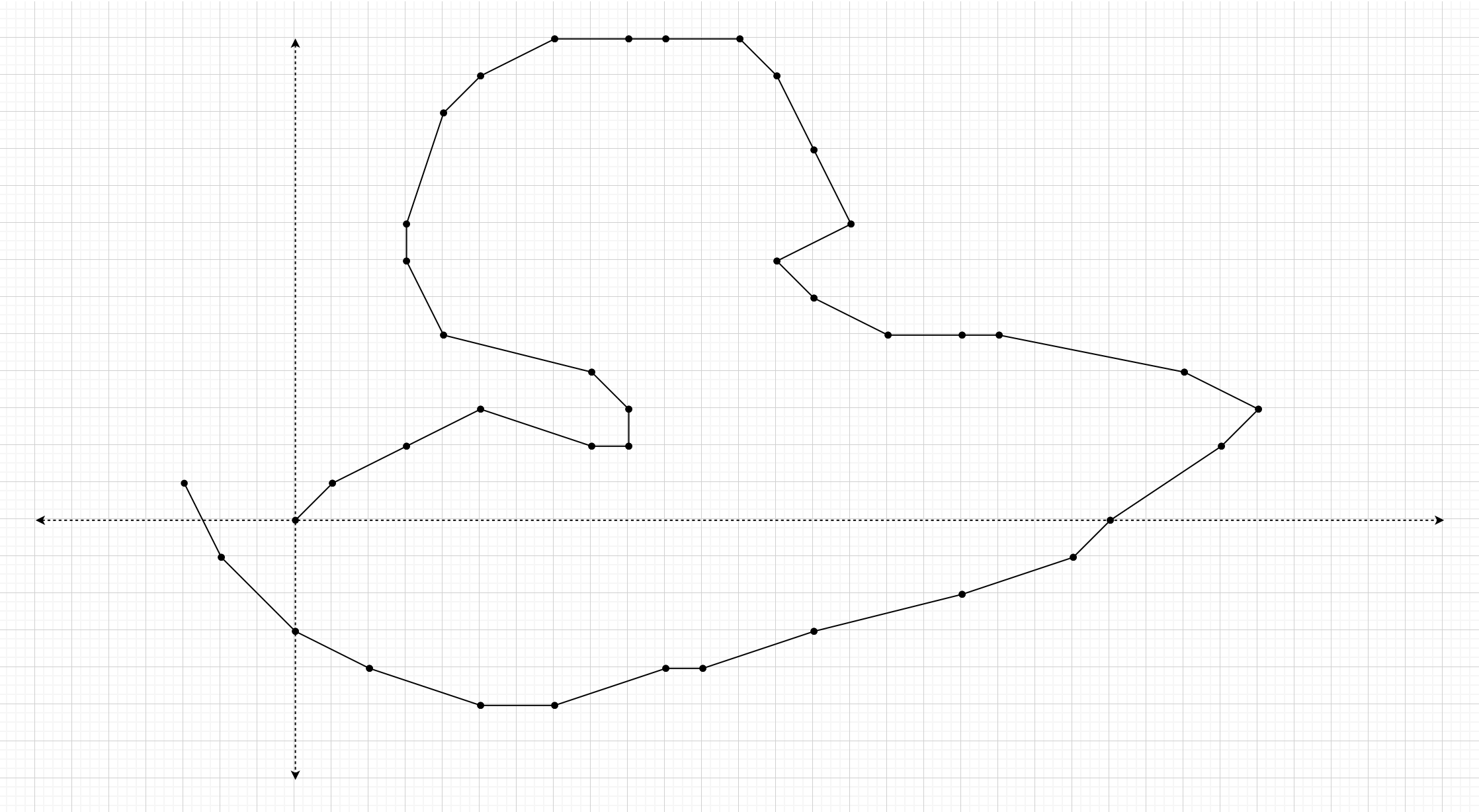
위 그림은 알고리즘 예시 데이터에 서술한 좌표 40개 목록이다. 위 경로를 한계치 40°로 압축한 결과는 다음과 같다.

19개 좌표로 압축되었다.

겹쳐서 보면 위와 같은 형태로 나온다.
※ 압축률은 경로의 형태에 따라 다르다. 직선구간이 많을 수록 많이 압축되며, 곡선구간이 많을 수록 적게 압축된다.
※ 정확도는 일치구간의 정도에 따라 다르다. 허용하는 각이 넓을 수록 정확도가 떨어지지만 압축률이 올라가며, 허용하는 각이 좁을 수록 정확도가 높지만 압축률은 떨어진다.
'Programming > Algorithm' 카테고리의 다른 글
| [Algorithm] 이동 평균 필터 (Moving average filter) (0) | 2021.12.04 |
|---|---|
| [Algorithm] 선형 보간법 (Linear interpolation) (0) | 2021.04.22 |
| [Algorithm] 지구에서 두 점 사이의 중간지점 구하기 (1) | 2020.09.15 |
| [Algorithm] 지구에서 두 점 사이의 방위각 구하기 (0) | 2020.09.07 |
| [Alogrithm] 지구에서 두 점 사이의 거리 구하기 (2) | 2020.08.25 |




댓글