선형 보간법 (Linear interpolation)
선형 보간법을 구현하는 방법에 대해 알아보자.
선형 보간법이란?
선형 보간법은 1차원 직선상에서 두 점의 값이 주어졌을 때 그 사이의 값을 추정하기 위해 직선 거리에 따라 선형적으로 계산(비례식)하는 방법이다.
선형 보간이 필요한 상황

위 사진을 보면 점 a와 b가 양쪽에 있고, 그 사이에 점 c가 있다. a와 b의 좌표는 각각 (2, 1)와 (7, 4)로 미리 알고있는 상황이며 c는 a와 b사이의 어느 한 지점이라는 점만 알고 있다.
이와 같은 상황에서 점 c의 x좌표가 임의로 주어졌을 때 선형 보간법을 사용하면 점 c의 y좌표까지 알아낼 수 있다.
선형 보간법을 적용하는 방법
선형 보간법을 적용하는 방법은 다음과 같다.

사진을 보면 a와 b가 어느 좌표에 있는지 알 수 있지만 c의 좌표가 어디인지는 확실하게 알 수 없다. 그저 "a와 b 사이의 어딘가" 라는 점만 알 수 있다.
이 때 점 c의 x 좌표를 임의로 지정하면 선형 보간법을 사용하여 점 c의 y 좌표까지 알아낼 수 있다.
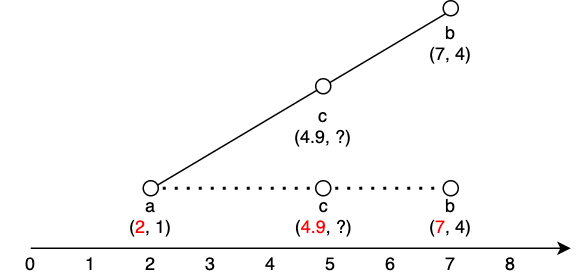
점 c의 x좌표를 4.9로 임의로 정하면 점 a, b, c의 x 좌표(2, 4.9, 7)를 모두 알 수 있는 상태가 된다.
배율 계산을 위해 x 좌표만 가지고 일렬로 늘어뜨려보자. (위 사진에서 실선으로 표시한 부분)

전체거리(d = b - a)를 구하고 시작점과 c 사이의 거리(d1 = c - a)도 구한다. 각각 5, 2.9 라는 숫자가 나오는데 d1에 대한 d의 배율을 구한다.
d1 / d = 2.9 / 5 = 0.58 이므로 백분율로 환산하면 58%을 의미한다.
즉, a로부터 b 방향으로 전체거리(b - a)의 58% 만큼 움직이면 c가 나온다는 뜻이다.
배율을 구했으니 이제 c의 y 좌표를 계산할 수 있다.

a의 y 좌표와 b의 y 좌표 사이의 거리를 구한 후 위에서 구한 배율을 곱한 뒤 a의 y 좌표를 더하면 c의 y 좌표를 구할 수 있다. 답은 2.74다.
결과적으로 선형 보간법을 사용하면 점 a(2, 1)와 점 b(7, 4) 사이의 점 c의 x 좌표가 4.9 일 때 y 좌표는 2.74 라는 결론을 도출할 수 있다.
알고리즘 적용
const a = { x : 2, y : 1 };
const b = { x : 7, y : 4 };
// 배율
const r = mag(a.x, b.x, 4.9);
// 결과
const y = a.y + (b.y - a.y) * r;
function mag(ax, bx, x) {
const d = bx - ax;
const d1 = x - ax;
return d1 / d;
}
// 실행결과
// y = 2.74
추가적으로 배율 계산에 방향성(+- 구분)을 포함하고 싶으면 mag 함수를 아래처럼 변경하면 된다.
function mag(ax, bx, x) {
const d = bx - ax;
const d1 = x - ax;
let m = d1 / d;
// + => - 부호 반전
if (d < 0) {
m *= -1;
}
return m;
}관련 문서
선형 보간법 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 선형 보간법(線型補間法, linear interpolation)은 끝점의 값이 주어졌을 때 그 사이에 위치한 값을 추정하기 위하여 직선 거리에 따라 선형적으로 계산하는 방법이
ko.wikipedia.org
Linear interpolation calculator
Linear interpolator Brought to you by Need to make sense of data? We can help.
www.johndcook.com
'Programming > Algorithm' 카테고리의 다른 글
| [Algorithm] Leaky bucket (처리량 제어기) (0) | 2025.03.11 |
|---|---|
| [Algorithm] 이동 평균 필터 (Moving average filter) (0) | 2021.12.04 |
| [Algorithm] 지구에서 두 점 사이의 중간지점 구하기 (1) | 2020.09.15 |
| [Algorithm] 지구에서 두 점 사이의 방위각 구하기 (0) | 2020.09.07 |
| [Alogrithm] 지구에서 두 점 사이의 거리 구하기 (2) | 2020.08.25 |




댓글